Profesor Andrzej Kossakowski został laureatem nagrody Fundacji na rzecz Nauki Polskiej za rok 2019 w obszarze nauk matematyczno-fizycznych i inżynierskich za „rozwinięcie teorii kwantowych układów otwartych”. Tym samym dołączył do listy wybitnych polskich fizyków teoretyków, którzy zostali uhonorowani nagrodą FNP.
Andrzej Kossakowski urodził się w lutym 1938 roku we Lwowie. Zaskakiwał czasami kolegów z zagranicy mówiąc, że urodził się w Polsce, następnie Lwów znalazł się w ZSSR, a teraz jest miastem na terenie Ukrainy. Jego kariera naukowa jest od samego początku związana z Uniwersytetem Mikołaja Kopernika w Toruniu, gdzie w latach 1955–1960 studiował fizykę, w roku 1966 obronił pracę doktorską, a w 1972 r. uzyskał habilitację z fizyki teoretycznej.
Jego zainteresowania naukowe koncentrowały się wokół fundamentalnych problemów fizyki kwantowej. Aby docenić wagę osiągnięć Laureata warto je zestawić z kluczowymi osiągnięciami w dziedzinie mechaniki kwantowej. Mechanika kwantowa powstała na początku XX wieku i dokonała przewrotu w naszym rozumieniu świata. W szczególności wyjaśniła strukturę widm atomowych obserwowanych przez fizyków w laboratoriach. Nie dało się tego wyjaśnić na bazie teorii, których podstawą była dotychczasowa fizyka zwana teraz „fizyką klasyczną”. Stworzenie nowej fizyki – fizyki kwantowej – wymagało prawdziwego geniuszu. Twórcy nowej teorii musieli porzucić dotychczasowe intuicje, przyzwyczajenia, a nawet język. W roku 1926 Erwin Schrödinger zaproponował nowe równanie, które z jednej strony opisuje własności obiektów kwantowych (np. atomów), a z drugiej strony przewiduje, w jaki sposób układ kwantowy będzie zmieniał się w czasie. Równanie to, nazwane natychmiast równaniem Schrödingera, stało się fundamentem nowej teorii. Każdy student fizyki zapoznaje się z nim na pierwszym kursie mechaniki kwantowej. W roku 1927 Lev Landau (genialny teoretyk z Petersburga – ówczesny Leningrad) podał równanie ewolucji dla tzw. stanów mieszanych wprowadzając obiekt nazywany macierzą gęstości, a odpowiednie nowe równanie znane jest jako równanie von Neumanna (John von Neumann podał matematyczne sformułowanie nowej teorii na początku lat 30.). Macierz gęstości to jeden z ulubionych obiektów Laureata, o czym mogli się przekonać redaktorzy kilku mediów, którym Laureat udzielał wywiadów. Z kolei w roku 1928 Paul Dirac (jeden z największych fizyków w historii) podał relatywistyczną wersję równania ewolucji kwantowej, tzn. zgodną z teorią względności Einsteina. Wspaniały gmach mechaniki kwantowej został ukończony. Schrödinger i Dirac zostali uhonorowani Nagrodą Nobla w roku 1933, a Landau w roku 1962. Pominąłem w tej krótkiej opowieści Wernera Heisenberga (nagroda Nobla 1932 r), który jest również jednym z twórców teorii kwantowej. Natomiast jego wkład do teorii nie ma bezpośredniego związku z dokonaniami Laureata.
Równania Schrödingera i von Neumanna posiadają szczególną cechę – są odwracalne w czasie, tzn. proces fizyczny, który formalnie przebiega „do tyłu” w czasie, jest również fizycznie dopuszczalny. Jest to własność tzw. układów zamkniętych, które nie wymieniają energii z otoczeniem.
A co jeśli układ nie jest zamknięty? Należy podkreślić, że każdy realistyczny układ fizyczny jest układem otwartym. Takich właśnie układów – nazywamy je otwartymi – dotyczą badania Laureata. Dynamika układów otwartych przestaje być odwracalna w czasie. Typowym przykładem takiego procesu jest emisja spontaniczna, kiedy to atom przechodzi spontanicznie ze stanu wzbudzonego do stanu podstawowego i w efekcie emituje promieniowanie. Problem ten był „atakowany” przez wielu znakomitych badaczy. Zaproponowano różne podejścia oparte na tzw. równaniach „master”. Niektóre z tych równań dawały przewidywania zgodne z eksperymentem. Inne okazywały się matematycznie niespójne i dawały nonsesowne wyniki. Główny problem polegał na tym, że nie był znany uniwersalny przepis jak skonstruować równanie tego typu.
Andrzej Kossakowski rozpoczął swoje badania w tej dziedzinie pod koniec lat 60. ubiegłego wieku. Pierwsze ważne rezultaty dotyczące struktury tego równania Laureat opisał w swoich artykułach opublikowanych w 1972 r. (m. in. w Reports in Mathematical Physics wydawanym w Toruniu; obecnie redaktorem naczelnym jest prof. Andrzej Jamiołkowski). Na początku lat 70. Laureat wyjechał do Stuttgartu na zaproszenie prof. Hermana Hakena. Pobyt w Stuttgarcie zaowocował kolejnymi ważnymi kontaktami naukowymi. Kossakowski poznaje Vittorio Goriniego z Mediolanu, który staje się jego bliskim współpracownikiem i przyjacielem (ostatnio regularnie odwiedza Laureata). Dzisiaj na nikim to nie robi wrażenia, ale w roku 1972 podróż z obywatela PRL z RFN do Mediolanu była nietrywialnym przedsięwzięciem logistyczno-administracyjnym. W roku 1974 Kossakowski razem z Gorinim jadą do Austin w Teksasie na zaproszenie prof. Sudarshana. Tam powstaje fundamentalna praca, która została opublikowana w 1976 r. w "Journal of Mathematical Physics" Completely positive dynamical semigroups of N‐level systems. Praca Laureata ukazała się zatem dokładnie 50 lat po pracy Schrödingera. Praca ta pokazuje, jaka jest najogólniejsza postać równania, które opisuje ewolucję otwartego układu kwantowego. Poniżej zdjęcie słynnego równania z oryginalnej pracy z Journal of Mathematical Physics:
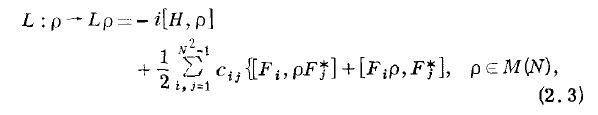
Równanie to jest konsystentne matematycznie, a jego przewidywania zostały doskonale potwierdzone w wielu eksperymentach. Praca ta ma trzech autorów, ale Laureat odgrywał w niej wiodącą rolę i cała koncepcja pracy oparta jest na jego wcześniejszych wynikach z początku lat 70.
Co ciekawe w tym samym roku ukazuje się praca Görana Lindblada ze Sztokholmu „On the generators of quantum dynamical semigroups” opublikowana w Communications in Mathematical Physics. Praca ta w istocie zawiera dokładnie taki sam wynik jak praca Gorini-Kossakowski-Sudarshan. Zaproponowane równanie weszło na stałe do kanonu fizyki teoretycznej i nosi obecnie nazwę równania Goriniego, Kossakowskiego, Sudarshana, Lindblada (GKLS master equation). Równanie GKLS obok równania Schrödingera, von Neumanna i równania Diraca należy do najważniejszych równań mechaniki kwantowej.
Obecnie równanie GKLS odgrywa istotną rolę w kwantowej teorii informacji (to również polska specjalność -- trzy nagrody FNP: (2008) prof. Ryszard Horodecki, (2011) prof. Maciej Lewenstein, oraz (2013) prof. Marek Żukowski). Warto podkreślić, że teoria ta została również zapoczątkowana w Toruniu profetyczną pracą profesora Romana Ingardena (wieloletniego kierownika Zakładu Fizyki Matematycznej i Statystycznej) „Quantum Information Theory” opublikowaną w Reports on Mathematical Physics w tym samym roku (1976), co praca Laureata. Równanie GKLS umożliwia modelowanie procesów takich jak dekoherencja i dyssypacja. Procesy te odgrywają istotną rolę w kwantowej komunikacji, kryptografii i kwantowym przetwarzaniu danych. Pokazuje to, że odkrycie Laureata posiada nadal potężny potencjał aplikacyjny.
W roku 2016 Zakład Fizyki Matematycznej zorganizował 48. Sympozjum Fizyki Matematycznej „Gorini-Kossakowski-Lindblad-Sudarshan Master Equation - 40 Years After”. W Sympozjum uczestniczyło około 100 fizyków, w tym najwięksi eksperci z teorii kwantowych układów otwartych. Honorowymi gośćmi Sympozjum byli Vittorio Gorini, Andrzej Kossakowski i George Sudarshan. Niestety Göran Lindblad nie mógł uczestniczyć w tym wydarzeniu, ale przysłał list wspominający wydarzenia sprzed 40 lat. Okazuje się, że Göran Lindblad uczestniczył w Sympozjum Fizyki Matematycznej w Toruniu w roku 1974 i 5 grudnia wygłosił referat, na którym zaprezentował wyniki swoich badań. W tym czasie Andrzej Kossakowski przebywał w Teksasie z pracą gotową do wysłania do publikacji. Po powrocie do kraju i prezentacji swoich wyników dowiedział się od prof. Woronowicza (nagroda FNP w roku 1993) o wynikach Lindblada. Co ciekawe Kossakowski i Lindblad do tej pory się nie spotkali.
Co ciekawe w tym samym roku ukazuje się praca Görana Lindblada ze Sztokholmu „On the generators of quantum dynamical semigroups” opublikowana w Communications in Mathematical Physics. Praca ta w istocie zawiera dokładnie taki sam wynik jak praca Gorini-Kossakowski-Sudarshan. Zaproponowane równanie weszło na stałe do kanonu fizyki teoretycznej i nosi obecnie nazwę równania Goriniego, Kossakowskiego, Sudarshana, Lindblada (GKLS master equation). Równanie GKLS obok równania Schrödingera, von Neumanna i równania Diraca należy do najważniejszych równań mechaniki kwantowej.
Obecnie równanie GKLS odgrywa istotną rolę w kwantowej teorii informacji (to również polska specjalność -- trzy nagrody FNP: (2008) prof. Ryszard Horodecki, (2011) prof. Maciej Lewenstein, oraz (2013) prof. Marek Żukowski). Warto podkreślić, że teoria ta została również zapoczątkowana w Toruniu profetyczną pracą profesora Romana Ingardena (wieloletniego kierownika Zakładu Fizyki Matematycznej i Statystycznej) „Quantum Information Theory” opublikowaną w Reports on Mathematical Physics w tym samym roku (1976), co praca Laureata. Równanie GKLS umożliwia modelowanie procesów takich jak dekoherencja i dyssypacja. Procesy te odgrywają istotną rolę w kwantowej komunikacji, kryptografii i kwantowym przetwarzaniu danych. Pokazuje to, że odkrycie Laureata posiada nadal potężny potencjał aplikacyjny.
W roku 2016 Zakład Fizyki Matematycznej zorganizował 48. Sympozjum Fizyki Matematycznej „Gorini-Kossakowski-Lindblad-Sudarshan Master Equation - 40 Years After”. W Sympozjum uczestniczyło około 100 fizyków, w tym najwięksi eksperci z teorii kwantowych układów otwartych. Honorowymi gośćmi Sympozjum byli Vittorio Gorini, Andrzej Kossakowski i George Sudarshan. Niestety Göran Lindblad nie mógł uczestniczyć w tym wydarzeniu, ale przysłał list wspominający wydarzenia sprzed 40 lat. Okazuje się, że Göran Lindblad uczestniczył w Sympozjum Fizyki Matematycznej w Toruniu w roku 1974 i 5 grudnia wygłosił referat, na którym zaprezentował wyniki swoich badań. W tym czasie Andrzej Kossakowski przebywał w Teksasie z pracą gotową do wysłania do publikacji. Po powrocie do kraju i prezentacji swoich wyników dowiedział się od prof. Woronowicza (nagroda FNP w roku 1993) o wynikach Lindblada. Co ciekawe Kossakowski i Lindblad do tej pory się nie spotkali.
Miałem szczęście być studentem Laureata (pamiętam jego znakomite wykłady z elektrodynamiki), a później również pracować z Laureatem nad problemami kwantowego splątania i kwantowej ewolucji. Profesor Kossakowski pozostał entuzjastą fizyki teoretycznej. Może spędzać całe godziny dyskutując o fizyce i pasjonujących go problemach. Kilka lat temu przebywał przez semestr w Neapolu na zaproszenie profesora Giuseppe Marmo. Miałem wtedy okazję mieszkać w jego mieszkaniu przy via Diocleziano (w Neapolu przebywał wtedy również George Sudarshan). Spędziliśmy wtedy wiele godzin dyskutując i pracując nad kwantowym równaniem z pamięcią. Towarzyszyło nam czasami wino sycylijskie Corvo Rosso (chociaż częściej z oczywistych powodów Lacryma Christi del Vesuvio), które Laureat łączył z historią rodzinną, a dokładniej z przydomkiem „Korwin”.
Miesiąc temu (10 października) dotarła do nas fantastyczna informacja o nagrodzie Nobla dla Olgi Tokarczuk „za wyobraźnię narracyjną, która z encyklopedyczną pasją reprezentuje przekraczanie granic jako formę życia”. Niesamowita wyobraźnia, encyklopedyczna wiedza i przekraczanie granic matematyki i fizyki to również doskonała charakteryzacja twórczości Laureata. Ale to nie jedyny związek Laureata z naszą noblistką. Czytelnicy „Ksiąg Jakubowych” (Nagroda Literacka „Nike” 2015) zapewne pamiętają Kossakowskich, a szczególnie Antoniego (Moliwdę) Kossakowskiego herbu Ślepowron, przydomek Korwin. Otóż Andrzej Kossakowski jest powiązany rodzinnie z tą brawurowa postacią z kart „Ksiąg Jakubowych”.
Polski Nobel dla Andrzeja Kossakowskiego to oczywiście wielka radość i wzruszenie dla Wydziału, a szczególnie dla Katedry Fizyki Matematycznej, w której (dawnym Zakładzie Fizyki Matematycznej) Profesor pracował. Moim zdaniem wyniki Profesora Kossakowskiego należą do najważniejszych w polskiej fizyce teoretycznej XX wieku. Nagroda Nobla dla Olgi Tokarczuk pokazuje, że są nadal większe nagrody do zdobycia. Byłaby to też idealna okazja do spotkania Kossakowski-Lindblad w Sztokholmie.
Prof. dr hab. Dariusz Chruściński – kierownik Katedry Fizyki Matematycznej Wydziału Fizyki, Astronomii i Informatyki Stosowanej UMK.
